Russian Second stand report (poster 2) First stand report (poster 1)


  A.V.Shestopalov         Program


Simulation of Rock Behavior under Load Using Numerical Methods and Cell Automaton Algorithm


- Report of International Conference "CADAMT'2001" (March 29-31, 2001, Tomsk, Russia).



Respected colleagues, ladies and gentlemens.




Slide 1 		Slide 2
Slide 3 Slide 4
Slide 5
Rock mechanics in depth where spontaneous failure of rockmass end part occurs is a new area of application of synergetics (slide 1).

The "rock mass - opening (cavity)" is an open system that may be far from mechanical equilibrium at big depth (slide 2).

Coal seam edge self-destruction is a typical problem of synergetic (slide 3).

The self-destruction proceeds from the surface to the rock mass depth and lasts till mechanical equilibrium is restored due to generation of a post-failure coal zone (slide 4).

If this zone is reduced critically or eliminated, another self-destruction cycle starts and proceeds at sound rate till mechanical equilibrium is re-established (slide 5).

Slide 6 Slide 7
Slide 8 Slide 8
Arising of a slip area in the coal seam edge is interpreted as generation of dissipative structures (slide 6).

It is practically impossible to describe in words the evolution of self organizing dissipative structure (slide 7).

Let us use the method of unmobile cell automata to visualize the process (slide 8).

We suggest that a system of 4 biharmonic differential equations should be substituted for the cell automaton. The equation are solved by numerical methods, e.g. method of end elements, but using a cell automaton algorithm.


Slide 9
The area of solution continuity (slide 9) is a half-plane with an infinitely far border D=100% of pressure function and a border in the form of a straight line D=0%.





Slide 10
Mathematical model for the "coal seam-opening" system is generally reduced to solution of problems of fragile failure under three energy fluxes, i.e. rock pressure, filtrating gas pressure and loose mass weight pressure (slide 10). Appearance of internal sources for the last two fluxes may be jump-like only.



Slide 11
The solution algorithm (slide 11) says that function for the total pressure D(x,y) should be found at each iteration in the simulation area that satisfies the system of four biharmonic differential equations including an equation with pressure function D=F(Ô,P,G,x,y), where Ô, P and G are pressure functions of the remaining three equations in the above-mentioned system. Only one of the above listed functions may be present in one equation, x and y are space coordinates. Each solution of every biharmonic equation consists of solutions of 2 Poisson harmonic equations according the same algorithm.






Slide 12
Final goal of the equation system solution analysis is to find coordinates of a cell (area) satisfying certain conditions that are the same for all cells (slide 12). If the criterion is satisfied in some area, we change (e.g. decrease strength or increase gas permeability) properties of the medium and set internal sources for the respective pressure function. Changes of boundary conditions in solution continuity area for all the 4 biharmonic equations precede solution of the mentioned equation system.




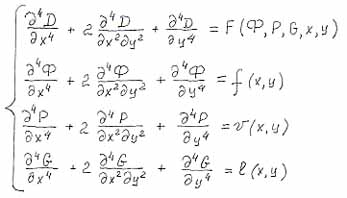
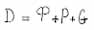
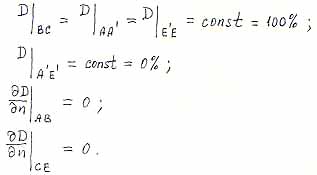
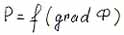
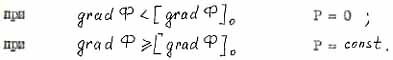
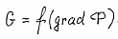
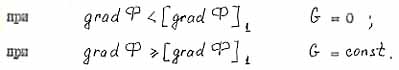
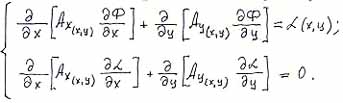
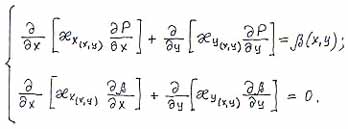
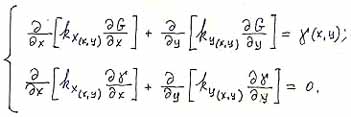
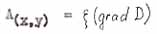
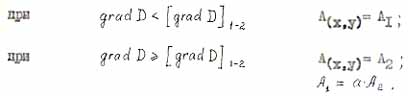
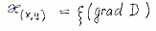
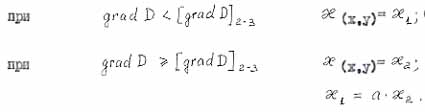
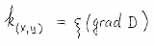
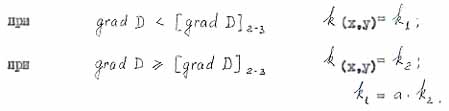
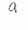
- scale factor.

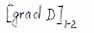
The step of post-failure development has at least two critical points:
- pseudomelting criterion;
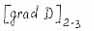
- pseudoboil criterion.


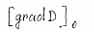
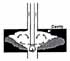
Slide 13
Self-organization of the front of the process under simulation (slide 13) happens during the solution spontaneously (by previously unknown inertia) as a result of identical non-linear (jump-like) changes in the simulated medium between the solutions. As cracks grow and reach fundamental length coal methane emission and permeability increase simultaneously and step-wisely.
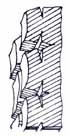
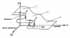
At the first critical point a new substance (methane) is generated at the tip of the growing crack. At the second point the methane amount is so large that all of it cannot filtrate into the opening and induces crack growth.


Slide 14 Slide 15
The author demonstrates that the end part of a rockmass is a fractal (slide 14, 15), i.e. a multi-level self-organizing system for technogenic self-propelling fractures in which the loss of shear stability occurs in a self-consistent manner at micro-, meso-, macro- and mega-scale levels.

Thank for attention.