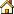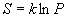Московский государственный университет им.М.В.Ломоносова
Международный междисциплинарный симпозиум "Фракталы и прикладная синергетика" ФиПС-03
КРУГЛЫЙ СТОЛ
"Проблема открытости сложных эволюционирующих систем"

Доклад 20.11.2003г. (16:50-17:10)

Свентицкий И.И.

Замкнутость эволюционирующих систем и энергетическая экстремальность самоорганизации

Сравнительно успешное развитие физико-химических и математических научных знаний сглаживают остроту существующих в них фундаментальных проблем. Рассмотрение проблемы открытости - закрытости (замкнутости) самоорганизующихся эволюционирующих систем способствует выявлению и решению этих проблем. Это относится, прежде всего, к возникшим во второй половине Х1Х-го столетия, проблемам, связанными с началами (законами) равновесной термодинамики и эволюцией сложных самоорганизующихся систем разной природы (физико-химической, биологической и социальной).

Проблема закрытости - открытости систем зародилась в термодинамике. Первое и второе ее начала обоснованы применительно к идеализированной закрытой системе, не обменивающейся с внешним пространством ни веществом, ни энергией. В иных основных разделах физики этому аспекту анализа систем до недавнего времени не уделялось внимания, очевидно, в связи с тем, что реальные природные системы в разной мере являются открытыми и, в то же время, в определенном отношении замкнутыми системами. Распространение приложения второго начала термодинамики на природные самоорганизующиеся системы [1, 2] обусловило возникновение упомянутых проблем.

Наиболее обостренно была воспринята проблема "вопиющего" [3] противоречия между эволюцией природы по второму началу термодинамики (ВНТД) и теорией биологической эволюции. По ВНТД, в соответствии с определением энтропии, эволюция природы имеет общую направленность к разрушению структур, деградации энергии, непрерывному и повсеместному росту энтропии. По теории биологической эволюции (дарвиновской, синтетической) живая природа развивается в диаметрально противоположном направлении - к развитию и совершенствованию структур и функций организмов и их сообществ, накоплению в них свободной (работоспособной) энергии.

Вторая общефизическая проблема, связанная с ВНТД, состоит в принципиальной не согласованности ВНТД с динамикой иных основных разделов физики. Она выявлена теоретически (математически) при обосновании теоремы возврата Пуанкаре-Мисры [3]. При рассмотрении этой проблемы в [3] высказано предположение о том, что для согласования ВНТД с динамикой основных разделов физики, вероятно, придется их принципиально переработать. Очевидно, этой проблемой обусловлены исследования по развитию физической теории открытых систем, в частности, статистической теории открытых систем [4]. Как будет рассмотрено далее, необходимости в создании такой теории при успешном развитии самоорганизации (синергетики) нет в связи с тем, что в теоретических основах основных разделов физики (классической, статистической и квантовой механике; оптике, релятивистской электродинамике) в качестве исходных положений использованы феноменальные принципы - Ферма, наименьшего действия. Сущность этих принципов противоположна сущности ВНТД. В неявном виде, в виде волновой функции и гамильтониана, сущность феноменальных принципов входит в главные уравнения этих разделов физики.

Третья термодинамическая проблема состоит в не согласованности ВНТД с третьим началом термодинамики (ТНТД). Согласно первоначальному определению теоремы Нернста - ТНТД - при приближении абсолютной температуры к нулю рост энтропии прекращается. Это определение уточнил М. Планк: при приближении абсолютной температуры к нулю энтропия также приближается к нулю (теорема Нернста-Планка - ТНТД). 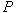Это определение обосновано тем, что в соответствии с формулой Больцмана, предложенной Планком, с приближением температуры к нулю термодинамическая вероятность () приближается к единице:

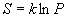, (1)

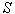где: - энтропия, 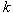- постоянная Больцмана.

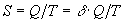Однако, такое определение ТНТД не согласуется с тепловым определением энтропии по формуле Клаузиуса:

, (2)

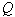где: - количество теплоты, 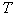- температура ее содержания 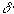- вариация. Из формулы (2) видно, что при приближении Т к нулю, энтропия будет приближаться не к нулю, а к бесконечности. Эта проблема видна также и из исходного аналитического выражения ВНТД - формулы Карно для определения теоретического КПД тепловой машины ():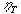

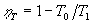, (3)

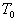где: - температура теплоносителя на выходе из машины, 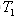- температура теплоносителя на входе в машину.

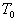Из практики конструирования тепловых машин и формулы (3) следует, что чем выше разность температур на входе и выходе из машины, тем выше КПД тепловой машины, тем выше эксергия (свободная энергия, работоспособность) используемой в машине теплоты, тем ниже ее энтропия. При устремлении и 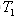к нулю работоспособность (эксергия) теплоты, используемой в машине, уменьшается, а энтропия возрастает. В этом подтверждение на основе формулы Карно проблемы не согласованности ВНТД с ТНТД.

Открытость - замкнутость эволюционирующих систем целесообразно рассматривать в следующих наиболее важных отношениях: обмена веществ, энергообмена, обмена информацией. Наиболее характерные самоорганизующиеся системы - живые системы. Важной феноменальной особенностью всех без исключения видов организмов является их высокая потенциальная способность к размножению, принятая Ч. Дарвиным в качестве исходного положения при разработке теории биологической эволюции. В тоже время, виды организмов являются закрытыми системами, в отношении основной биологической информации - наследственной, генетической информации - так как межвидовое скрещивание, как известно, принципиально затруднено.

Разные фазы онтогенетического развития организмов имеют разную меру открытости - замкнутости, как в отношении энергообмена, так и обмена веществ. Семена и споры автотрофных организмов до прорастания закрыты оболочками, препятствующими активному обмену зародышевой части энергией и веществом, как с внешней средой, так и внутри семени. Запуск такого обмена происходит благодаря внешней информации, характеризующей благоприятность внешней среды для развития организма. Семена диких растений (сорняков) могут многие годы сохраняться в почве.

В начальный период прорастания семян происходит гетеротрофное питание проростка за счет питательных веществ семени. В этот период растительный организм закрыт в отношении обмена энергией с внешней средой. Только после формирования фотосинтетического аппарата, проросток переходит к автотрофному питанию энергией оптического излучения (света). При благоприятном субстрате для гетеротрофного питания клеточная культура фототрофных растений может не переходить на автотрофное питание.

Наиболее развитые растительные ценозы и экосистемы, как правило, более замкнуты в отношении обмена веществ по сравнению с менее развитыми подобными системами. Наименьший обмен веществом с внешним миром имеет место в климаксных экосистемах. Круговорот веществ в экосистемах, как известно, происходит благодаря жизнедеятельности в них трех групп видов организмов. Эти группы состоят из: продуцентов - автотрофных организмов - в основном фотосинтезирующих растений, макроконсументов - гетеротрофных животных и микроконсументов или редуцентов - разлагателей - преимущественно бактерий и грибов [5]. В развитых экосистемах в наибольшей мере сбалансированы эти три, взаимно дополняющие друг друга в круговороте веществ и использовании энергии, группы организмов.

По уровню замкнутости экосистемы в отношении обмена веществ можно судить о полноте (эффективности) использования в ней свободной энергии первичной продуктивности - свободной энергии, накопленной растениями в созданных ими органических веществах. С повышением замкнутости экосистемы по обмену веществ возрастает также эффективность использования ею свободной энергии, накопленной в результате преобразования растениями энергии света в химическую энергию органических веществ. Если принять во внимание очень яркое выражение сущности экологии в [5, с. 53]: "Экология, по сути дела, изучает связь между светом и экологическими системами и способы превращения энергии внутри системы", то можно придти к важному выводу о большом значении показателя (критерия) открытости - закрытости (замкнутости) экосистем для развития теоретических начал экологии.

Современная экология развивается на эмпирической основе. Ее закономерности, правила, законы, принципы и т.п.; которых по данным Н.Ф. Реймерса около 250 [6], обоснованы эмпирически. Несмотря на их большое количество "... и они не перекрывают друг друга". Анализ попыток развития теоретических основ экологии приводит к заключению, что принципиальная трудность этого развития обусловлена упомянутой выше проблемой противоречия между эволюцией природы по ВНТД и теорий биологической эволюции. Исходные положения теоретических основ экологии должны быть заимствованы из более общих смежных отраслей знаний - физики и общей (теоретической) биологии. В физике наиболее важным в общем методическом (методологическом) отношении законом является ВНТД. В общей биологии теоретической основой считают теорию биологической эволюции [7]. Эволюционисты не случайно считают, что "эволюцию невозможно понять в не экологии". Очевидно, справедливо и обратное: экологию невозможно понять без учета основных положений эволюции. "Вопиющее противоречие" между эволюцией природы по ВНТД и теорией биологической эволюции не позволяет использовать эти общие теоретические начала, в качестве исходных в теории экологии. Как будет рассмотрено далее, разрешение этого противоречия открывает возможность развития теоретической биологии.

С эффективностью использования свободной энергии экосистемой а, следовательно, и с мерой ее замкнутости - открытости в отношении обмена ее с окружением энергией и веществом, связаны две наиболее важные эмпирические закономерности экологии: заполнения трофических (экологических) ниш и детерминизм сукцессионного процесса. Сущность первой: если в экосистеме где-то имеются запасы (потоки) доступной свободной энергии - пищи для организмов, то они обязательно там появятся и будут ее использовать. В соответствии со второй - каждый последующий естественно сменяющийся видовой состав экосистемы создает или поддерживает при одном и том же количестве (потоке) энергии большее количество живой массы и/или большее количество информации (видового состава). Эти эмпирические закономерности естественнонаучно не объяснены и на первый взгляд логически не связаны. Как будет показано далее, они взаимно обусловлены в соответствии с принципом энергетической экстремальности самоорганизации.

Одна из сложных эволюционирующих систем, доступных для наблюдений - биосфера. Согласно современным представлениям самоорганизация ее биологического этапа эволюции проходила гармонично [8, с.51-52]: "Показано, что фазе биологической эволюции соответствует полная гармония развития по ключевым параметрам эволюции, а фазе социальной эволюции - полное их рассогласование". Антропогенное вмешательство в процессы биосферы нарушает ее самоорганизацию. Оно может привести к нарушению устойчивости биосферы. Основные, негативные воздействия человеческого общества на функционирование экосистем и биосферы имеют, не случайно, энергетическую природу.

Живая часть биосферы с ее физическим окружением практически замкнута в отношении обмена веществ. Вещество в нее из внешнего окружения (космоса) поступает только в виде метиоритов. Почти по замкнутому циклу в живой части биосферы обращаются доли процента, от общего количества содержащихся на Земле, таких важных биофильных элементов, как азот и углерод [9, 10]. Это обусловлено, очевидно, тем, что поддержание этих элементов в усвояемом для организмов состоянии требует затрат организмами и их сообществами свободной энергии. Внесение, например, избыточных доз азотных удобрений в почву, с целью повышения урожая, приводит к загрязнению ими природной среды из-за самопроизвольного удаления их из агроценоза.

Биосфера односторонне открыта для поступления в нее из космоса эксергии (свободной энергии) и, в то же время, замкнута для оттока эксергии из нее. Составляющие биосферу природные эволюционирующие экосистемы также не являются полностью закрытыми или полностью открытыми. Являясь, частично замкнутыми системами, они успешно эволюционирую. В них минимизирован обмен веществ с внешней средой. Это же относится и к биосфере.

От Солнца на Землю поступает общая мощность энергии солнечного оптического излучения ("света") примерно 170 х 1012 кВт. Около 34% ее отражается в космос. Остальная часть участвует в совершении работы по самоорганизации биосферы (на поверхности земли, в водной и воздушной среде). Эта энергия осуществляет круговорот воды и других веществ, без осуществления которого, невозможно функционирование биосферы. После совершения работы по самоорганизации биосферы, поступившая на Землю энергия приблизительно в том же количестве излучается в космос, чем объясняется стационарное тепловое состояние Земли. Исключение составляет мощность энергии поглощаемой и аккумулируемой растениями (примерно 3х1011 кВт), которая накапливается ими в процессе фотосинтеза в виде химической энергии органических веществ. Используя энергию не возобновляемых природных ресурсов - топлива - человек выделяет в виде тепла примерно 7х109 кВт. Эта антропогенная тепловая мощность примерно в 50 раз меньше, чем аккумулируется растениями.

Иной баланс Земли и биосферы в отношении качества энергии - содержания в ней энтропии или эксергии (свободной энергии). Поступающая на Землю низко энтропийная энергия солнечного излучения, соответствующая температуре излучающей поверхности Солнца, примерно 6000о, содержит до 94% эксергии. С Земли уходит такое же количество низко эксергетической, высоко энтропийной энергии излучения с температурой излучающей поверхности Земли около 300о.

В связи с этим, в развиваемой физике открытых систем [4], подобно как в термодинамике закрытых систем, обязательно возникнут проблемы обусловленные тем, что исходная модель открытой системы (как и замкнутой) принципиально не соответствует реальным природным системам, которые может отобразить в полной мере принцип энергетической экстремальности самоорганизации и прогрессивной эволюции. Этот принцип обоснован, как на микро уровне, так и на макро уровне.

В работах проф. МГУ А.П.Руденко в исследованиях на уровне элементарных открытых каталитических систем (на микро уровне) выявлено [11], что при преобразовании ими энергии, наряду с рассеянием энергии и ростом энтропии, совершается также за счет энергии основного энергопреобразующего процесса полезная работа по повышению неравновесности системы и уменьшению ее энтропии. Тем самым выявлена возможность решения проблемы противоречия между эволюцией природы по второму началу термодинамики и теорией биологической эволюции.

Решение этой проблемы выявлено и на макро уровне автором [12, 13] - путем обоснования закона (названного законом выживания), противоположного по своей сущности ВНТД. Этих два закона составляют принцип энергетической экстремальности самоорганизации, который тождествен принципу экстремального действия, обоснованному Л.Эйлером в 1744г. на основе принципа наименьшего действия.

Косвенная экспериментальная проверка реальности существования закона, противоположного по своей сущности ВНТД, успешно проведена на примере создания энергоэкономных электрических ламп для обеспечения фотосинтеза растений в искусственных климатических условиях. Этой проверкой одновременно показана высокая результативность использования этого закона для решения практических задач агроэнергетики. Эффективность впервые созданных электрических ламп для искусственного облучения (освещения) растений увеличена в 1,5-1,8 раза [13].

Проверка достоверности новых знаний (законов) традиционно проводится сопоставлением их с наиболее важными обще признанными законами природы, например с ВНТД. Если новые знания согласуются с соответствуютщим общепризнанным законом, то их достоверность признается. Если же они не согласуются, то достоверность новых знаний (закона) считается не подтвержденной. Однако, такая проверка достоверности справедлива только для случаев, когда уровень общности нового закона ниже уровня общности общепризнанного закона. Она не пригодна для проверки достоверности нового закона, общность которого равна или выше общности закона, принимаемого за эталонный.

Однако, наряду с общепризнанными общими законами природы, существуют феноменальные явления (феномены), которые надежно эмпирически или математически установлены, но современной наукой не объяснены. Они свидетельствуют о наличии еще не открытых законов природы высокого уровня общности. Использование новых знаний высокого уровня общности для объяснения феноменальных явлений - одна из возможностей выявления достоверности новых знаний.

Достоверность закона, противоположного по своей сущности ВНТД, подтверждена использования его для естественнонаучного объяснения следующих феноменов: золотого сечения, онтогении или биогенетического закона, высокой потенциальной способности всех видов (без исключения) организмов к размножению, фрактальных зависимостей и отображаемых ими объектов. Все эти феноменальные явления оказались природными энергоэффективными (энергоэкономными) процессами и структурами - механизмами или следствиями проявления закона, противоположного по своей сущности ВНТД [12, 13]. К числу таких феноменов относятся также феноменальные принципы, используемые в качестве исходных положений в основных разделах физики и химии: Ферма, наименьшего действия, Ле Шателье, закон (правило) электромагнитной инерции Ленца.

Тождественность принципа Ферма принципу наименьшего действия выявлена Г.С.Ландсбергом. Им показана возможность преобразования принципа Ферма в принцип экстремального действия [14, с.201]: "Для того чтобы принцип Ферма выражал действительное положение дел, ему надо дать более общую формулировку, чем это сделал сам Ферма; именно, ... может быть не только условием минимума, но и условием максимума ...". Реальность такого преобразования в [14] подтверждена геометрическими построениями. Из принципа Ферма выводятся все законы геометрической оптики и аналитические зависимости оптики, включая волновую функцию, которая используется в основных уравнениях: квантовой теории (уравнения Шредингера) и релятивистской электродинамики (уравнения Дирака). Как уже отмечалось, принцип наименьшего действия был преобразован в принцип экстремального действия Л.Эйлером.

Тождественность закона электромагнитной инерции Ленца принципу наименьшего действия видна из следующего. Закон электромагнитной инерции Ленца минимизирует переход магнитной энергии в электрическую и наоборот, а принцип наименьшего действия минимизирует переход потенциальной энергии в кинетическую и наоборот [15]. Принцип Ле Шателье был сформулирован по аналогии с законом электромагнитной инерции Ленца, что также подтверждает их определенную тождественность. В то же время, отличительная особенность принцип Ле Шателье в том, что он позволяет определить направленность реакции системы на внешние воздействия, направление смещения ее равновесия. Эта особенность принципа Ле Шателье имеет особо важную роль в решения существующих проблем биологической эволюции. Принцип Ле Шателье отображает приспособительную (адаптивную) реакцию природных систем к воздействиям внешней среды. Каждое действие внешней среды на систему вызывает в ней изменения ослабляющие эффект этого действия. Реакция природных систем на внешние воздействия в соответствии с принципом Ле Шателье возможна благодаря определенной замкнутости систем по отношению к внешней среде.

В процессах самоорганизации важная роль принадлежит явлению флуктуации. Вполне определенное направление смещения равновесия в соответствии с принципом Ле Шателье происходит, как на элементарном флуктуационном уровне, так и на всех последующих уровнях организации системы, взаимодействующей с внешней средой. Из этого можно заключить, что, чем сложнее структура самоорганизующейся системы, тем быстрее она приспосабливается к внешним воздействиям, тем быстрее она эволюционирует в соответствии с принципом Ле Шателье.

Это положение, имеющее очень большое значение для теории эволюции, подтверждают современные данные по изучению генетических структур организмов. Можно принять, что геном человека состоит из 30 тыс. генов. Геном мыши составляет 90% генома человека. Только 1% генома мыши отличается от соответствующих структур генома человека. Из этих, эмпирически установленных данных, можно придти к заключению о том, что со времени расхождения путей эволюции от общего предка человека и мыши скорость изменения их генетических структур принципиально различна. Геном человека увеличился более чем на 10%. За этот же эволюционный период геном мыши возрос только на 1%. В соответствии с этими данными, как и следовало ожидать, исходя из принципа Ле Шателье, генетические информационные структуры человека, как более сложной самоорганизующейся системы, эволюционировали в десять раз быстрее, чем подобные структуры мыши - существенно менее сложной системы.

Главный энергопреобразующий закон современной энергетики и физики - ВНТД - не может объяснить рассмотренные феноменальные принципы, используемые в качестве исходных положений в основных разделах физики. Физико-химические самоорганизующиеся системы по своим важным свойствам (например, энергетическим) более близки к живым, чем к системам не самоорганизующимся (равновесным) физико-химическим. Это - одно из важнейших исходных положений в решении долго не разрешавшихся, фундаментальных проблем физики и биологии. Физика (за исключением термодинамики) изучает самоорганизующиеся физико-химические структуры и процессы. Феноменальные принципы физики, составляющие ее исходную основу, по своей сущности противоположны ВНТД, и являются природными механизмами энергоэкономности, которые объединяет общий закон энергетической экстремальности самоорганизации.

В этом естественнонаучное подтверждение, теоретически (математически) доказанной в теореме Пуанкаре-Мисры, проблемы принципиальной не согласованности ВНТД с динамикой всех основных разделов физики и, одновременно, основа решение этой проблемы.

Автором обосновано решение третьей проблемы термодинамики - не согласованности второго и третьего начал термодинамики. Оно имеет ту же основу, что и решения двух других проблем, связанных с ВНТД. Как показано в [12, 13], возникшие при статистическом определении энтропии трудности в отношении знака правой части формул (1) и (2), можно разрешить, приняв два знака. При знаке минус формулы (1) и (2) будут соответствовать определению энтропии для самоорганизующихся (не равновесных) систем, а знак плюс - для определения энтропии равновесных (не самоорганизующихся) систем. 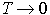Для этих двух случаев предельное значение энтропии при будет иметь значения для формулы (1) соответственно 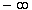и 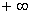, а для формулы (2) 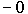, и .

В тоже время из третьего начала термодинамики следует принцип недостижимости абсолютного нуля температуры [16, с.136]: "... невозможен такой процесс, в результате которого тело могло бы быть охлаждено до абсолютного нуля (принцип недостижимости абсолютного нуля температур)". Это, казалось бы, явное противоречие, разъяснено в учебном пособии по термодинамике [17, с.157], в котором одна из глав посвящена отрицательной абсолютной температуре: "Нельзя отрицать возможность существования отрицательных абсолютных температур и исходя из третьего начала термодинамики". Действительно, недостижимость абсолютного нуля температуры приводит лишь к невозможности перехода через него от положительных к отрицательным абсолютным температурам, но не исключает возможность существования отрицательных абсолютных температур". В [17] сделана попытка показать возможность осуществления отрицательных абсолютных температур, без прохождения температуры через нуль. 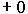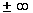Это возможно тогда, когда температура в направлении ее роста проходит по шкале в следующем последовательном порядке [17, с.158]: "Температура в направлении ее роста проходит на шкале в последовательном порядке значения: +0К, ..., +500К, ..., , ..., -500К, ..., -0К. Температура +1000К является промежуточной между +500К и -500К". Однако, при написании работы [17] считалось, что формулы (1) и (2) имели в правой части только один положительный знак. Для этого случая невозможно осуществить шкалу температур замкнутую через 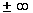, так как при этом в ней будет только правая ветвь: 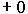и . 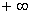Реализовать замкнутую последовательность температур, не проходящую через нуль, можно только в том случае, когда в правой части формул (1) и (2) для определения энтропии будет два знака: "+" и "-". По формулам (1) и (2) энтропия определяется как функция одной переменной (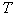). Это позволяет использовать аналогичную замкнутую шкалу и для энтропии (фиг. 1).
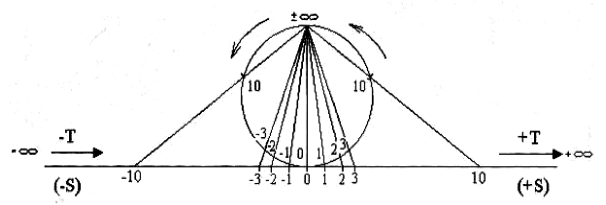
Фиг. 1. Диаграмма температур и энтропии не проходящих через абсолютный нуль, в соответствии с третьим началом термодинамики (теорема Нернста - Планка). Пояснения в тексте.

Рассмотренное решение проблемы не согласованности ВНТД и ТНТД одновременно подтверждает правильность выше рассмотренного решения на этой основе двух других проблем термодинамики и прогрессивной эволюции, а также достоверность принципа энергетической экстремальности самоорганизации.

Уместно обратить внимание на то, что аналитические выражения составляющих энергетической экстремальности самоорганизации - ВНТД и противоположного ему по сущности закону - могут различаться только знаком в правой части, как это имеет место в рассмотренных аналитических определениях энтропии. В термодинамических исследованиях не редки случаи, когда самопроизвольно (неосознанно) меняется знак на обратный и тем самым осуществляется неосознанный переход от ВНТД к противоположному ему по сущности закону (закону выживания). Известны случаи, когда, благодаря подобным ошибкам, на основе ВНТД, "решают" задачи, которые в действительности можно решить только на основе закона противоположного по сущности ВНТД.

В [17] рассмотрена система с отрицательной абсолютной температурой и показано, как осуществляются отрицательные абсолютные температуры в системе "элементарных магнитов". В [17] также описан пример экспериментального осуществления системы с отрицательной абсолютной температурой в 1951 г. Перселом и Паундом в экспериментах по изучению свойств системы ядерных спинов в очень чистых кристаллах фтористого лития. При рассмотрении термодинамики систем с отрицательной абсолютной температурой, выявлен ряд их специфических свойств, которых нет у обычных систем. Исходя из этих свойств, можно предположить, что системы с отрицательной абсолютной температурой не являются равновесными. При температурах близких к абсолютному нулю многие металлы и сплавы обладают свехпроводимостью и серхтекучестью [16]. Результаты изучения этих явлений свидетельствуют, что они обусловлены процессами самоорганизации на микро уровне - на уровне взаимодействий электронов и других элементарных частиц с кристаллической решеткой. Учет положений самоорганизации при изучении свехпроводимости и серхтекучест позволит ускорить развитиеие теории этих явлений.

Аналитически сущность решения рассмотренных трех проблем термодинамики закрытых систем и прогрессивной эволюции природы сводится к использованию в правой части формул: по тепловому определению энтропии (формула Клаузиуса) и статистическому определению энтропии (формула Больцмана, предложенная М. Планком) не только положительного, но и отрицательного знака. При положительном знаке эти формулы отображают закрытые равновесные (не самоорганизующиеся) системы, в которых энтропия возрастает, а при отрицательном знаке они описывают, в принципе открытые, самоорганизующиеся (не равновесные) системы, в которых энтропия уменьшается.

С выявлением энергетической экстремальности самоорганизации и решением на ее основе, более столетия не разрешавшихся, проблем равновесной термодинамики и эволюции природы можно считать разгаданным одно из крупных естественнонаучных заблуждений. Необоснованное распространение приложения ВНТД к самоорганизующейся природе привели во второй половтне Х1Х столетия к выводу о тепловой смерти Вселенной. В 1886г. о ней Л.Больцман говорил [2, с.11]: "Все попытки спасти Вселенную от этой тепловой смерти остались безуспешными, ...".

В отличие от других основных законов природы, ВНТД в связи с этим приобрел и до настоящего время играет важную мировоззренческую роль. И в наше время, к сожалению, этот вывод рассматривают как обоснованный некоторые ученые. Например, в [18, с.274] признается ведущая роль биоэнергетического прогресса в прогрессивной направленности эволюции: "...появление цивилизации на Земле или другой подходящей планете является неизбежным следствием биоэнергетического прогресса...". Однако, при этом делается необоснованный вывод о том, "...что появление цивилизаций во Вселенной является неизбежным следствием второго начала термодинамики и принципа наискорейшего спуска. Появление цивилизаций является как бы механизмом ускорения приближения Вселенной к равновесию, который без этого осуществлялся бы значительно медленнее". Появление цивилизаций нельзя признать следствием второго начала термодинамики. Напротив, прогрессивная эволюция противоречит этому началу и не может быть им объяснена. Существование и развитие самоорганизующейся природы, включая цивилизацию, не может влиять на "приближение Вселенной к равновесию". Это становится особенно ясным, если принять во внимание отсутствие влияния процессов биологического и антропогенного преобразования энергии на Земле на энергетические процессы Солнца, которые обеспечивают первичной энергией биосферу. Это с предельной четкостью понятно и из рассмотрения механизма гравитационного коллапса. "Принцип наискорейшего спуска" реально ничем не обоснован.

Рассмотренное естественнонаучное заблуждение, обусловленное необоснованным распространением приложения ВНТД к самоорганизующейся природе, используют для оправдания (подтверждения целесообразности) негативных социально-политических решений, в частности, "теории золотого миллиарда". Сторонники этой "теории" утверждают, что экологических условий Земли и ее ресурсов достаточно для комфортного проживания только одного миллиарда человек. Эта антигуманная теория, естественнонаучно не обоснованная, справедливо подвергается критике, например, в [8, 13, 19].

Исходя из ВНТД, сделан вывод о необратимости процессов природы, об их общей направленности к разрушению структур, деградации энергии, повсеместному и непрерывному росту энтропии в соответствии с определением этой величины. Со второй половины Х1Х столетия опубликованы сотни исследований, посвященных этой проблеме. Последовательный анализ большинства из этих работ приведен в [20]. Внимательное изучение результатов этого анализа позволяет сделать вывод о том, что никому из авторов работ, рассмотренных в [20], не удалось доказать обоснованную, исходя из ВНТД, необратимость. Даже в работах, из которых, на первый взгляд, можно сделать вывод о наличии такого доказательства, не исследованы ветви доказательств, которые, как справедливо показано в [20], могут привести к выводу об обратимости. Этот вывод подтверждают последовательное рассмотрение проблемы необратимости с позиций неравновесной термодинамики И. Пригожина в [3].

При рассмотрении гносеологических вопросов в основах квантовой механики Д.И. Блохинцевым еще в 60-х годах ХХ-го столетия по рассматриваемой теме сделаны содержательные прогнозы [21, с.586-587]: "Было бы неправильно полагать, что можно применять (или что в последствии станет возможным применить) к отдельным микроявлениям понятие классической причинности, пригодное для изолированных систем. Скорее всего, что такой изолированности в мире атомных явлений вообще не существует. ...В последствии могут обнаружиться такие новые физические явления, о которых мы сейчас не в состоянии подозревать и которые быть может позволят построить нестатистическую теорию микроявлений. Сочетания утверждений, представляющихся сейчас противоречивыми, могут гармонически согласовываться в будущем. Так, во времена расцвета классической термодинамики всякое утверждение о том, что тепло может само собой перейти от холодного тела к более теплому, было бы воспринято как, очевидно, не научное, противоречащее "второму началу" термодинамики. Но мы знаем, что позднейшее развитие примирило подобную возможность с классической формулировкой второго начала в новых рамках кинетической теории материи". Реальность этих прогнозов частично подтверждена в этой работе.

При обсуждении результатов обоснования принципа энергетической экстремальности самоорганизации и результатов решения проблем термодинамики и эволюции природы, иногда, стремясь подвергнуть сомнению эти результаты, говорят: "Теоретически можно обосновать все. Но Вы докажите это экспериментально, создайте "вечный двигатель", который запрещают начала термодинамики". В связи с этим целесообразно ознакомиться с мнением по этому вопросу Л.Больцмана - одного из основателей термодинамики - и Э.Маха - его оппонента.

Обращаясь в письме к Эрнсту Маху (от 01.10.1893) с просьбой ответить на вопрос - "Можете ли доказать невозможность ... perpetuum mobile, исходя из закона причинности?", Л.Больцман сообщает: "Я полагаю, что невозможность perpetuum mobile это чисто опытный закон, который в еще не подвергшихся проверке случаях может в любой момент быть опровергнут опытом. Мое мнение, что это чрезвычайно мало вероятно в отношении так называемого первого закона и, может быть, не слишком вероятно в отношении второго основного закона (для условий, достаточно отличающихся от исследованных), является чисто субъективным, недоказуемым" [2, с.183].

Так как письма Э.Маха к Л.Больцману не сохранились, то об ответе Маха можно судить лишь по содержанию следующего письма Больцмана к нему (от 26.10.1893): "Глубокоуважаемый коллега! Я радуюсь, что мы теперь совершенно одинакового мнения,... Теперь я вижу, что Вы в этом вопросе придерживаетесь точно такого же мнения, и я вполне удовлетворен" [2, с.187]. Как видим, теоретик фундаментальной науки и создатель теории термодинамики прямо не связывали теоретические обоснования и следствия начал термодинамики с возможностями создания вечных двигателей первого и второго рода. Очевидно, одному исследователь невозможно обосновать решение столетних проблем термодинамики и создать вечные двигатели, которые разработаны и испытаны другими учеными и изобретателями.

Например, Б.Б.Голицын еще в Х1Х столетии теоретически обосновал возможность преобразования высоко энтропийной теплоты с низкой эксергией непосредственно в высоко эксергетическую электрическую энергию с низкой энтропией [22]. Эта возможность не согласуется с началами термодинамики. В [23] опубликована практическая реализация этой возможности на основе нелинейного конденсатора, который теплоту окружающего воздуха непосредственно преобразует в электрическую энергию с КПД 0,32. Подобных примеров публикаций по осуществлению "вечных двигателей", основанных на использовании различных самоорганизующихся процессов и самоорганизованных структур, можно привести множество.

Исходной моделью при обосновании начал (законов) термодинамики использована идеализированная закрытая система, не имеющая обмена ни веществом, ни энергией с внешней средой. Эти начала приложимы только к равновесным не самоорганизующимся системам. Самоорганизующиеся системы, являясь диссипативными, могут функционировать и развиваться только при наличии энергообмена с внешней средой. Они не могут быть полностью закрытыми. Природные самоорганизующиеся системы могут быть частично замкнутыми в отношении обмена веществ, но открытыми для обмена энергией и информацией.

Столетние проблемы термодинамики и прогрессивной эволюции природы обусловлены не правомерным распространением приложения ВНТД и ТНТД к самоорганизующейся неравновесной природе. Они решены на основе главного принципа самоорганизации (синергетики) - энергетической экстремальности самоорганизации и прогрессивной эволюции, который надежно обоснован как на микро, так и на макро уровнях. Все природные самоорганизующиеся системы организованы и функционируют в соответствии с этим принципом. В них одновременно с деградацией энергии и ростом энтропии происходят противоположные процессы - концентрация свободной энергии и уменьшение внутренней энтропии за счет потребления свободной энергии (эксергии) из внешней среды.

Эта особенность реальных природных систем отражена в основных разделах физико-химических научных знаний, исключая термодинамику, на основе использования в качестве исходных положений феноменальных принципов: Ферма, наименьшего действия, Ле Шателье, закона электромагнитной инерции Ленца и др. Эти принципы в неявном виде (в виде гамильтониана, волновой функции оптики) входят в главные уравнения основных разделов физики. Общую сущность феноменальных принципов физики объединяет закон, противоположный ВНТД, который совместно с ВНТД входит в состав энергетической экстремальности самоорганизации и прогрессивной эволюции.

Литература

1. Второе начало термодинамики (С.Карно, В.Томсон-Кельвин, Р.Клаузиус, Л.Больцман, М.Смолуховский), М.-Л., Гостехтеоретиздат, 1934.
2. Больцман Л. Статьи и речи. М., Наука, 1970.
3. Пригожин И. От существующего к возникающему. Время и сложность в физических науках. М., УРСС, 2002.
4. Климантович Ю.Л. Статистическая теория открытых систем. Т.1, М., "Янус", 1995.
5. Одум Ю. Основы экологии. М., Мир, 1975.
6. Реймерс Н.Ф. Экология (теории, законы, правила, принципы, гипотезы). М., 1994.
7. Эволюция. М. Мир, 1981.
8. Иванов О.П. Причины различия эволюции биосферы и общества, экологические следствия и методология выхода. // Синергетика, т. 6, М., МГУ, 2003. - с.51-67.
9. Деви Э. Круговорот минеральных веществ. // Биосфера. М., Мир, 1972. - с.120-138.
10. Делвич К. Круговорот азота. // Биосфера. М., Мир, 1972. - с.105-119.
11. Руденко А.П. Саморганизация и синергетика. // Синергетика, т. 3, М., МГУ, 2000. - с.61-99.
12. Свентицкий И.И. Фундаментальные проблемы науки и истоки их решения. // Аграрная наука, 2001, N3, N4. - с.2-4, c.2-3.
13. Свентицкий И.И. Принципы энергосбережения в АПК. Естественнонаучная методология. М., ВИЭСХ, 2001.
14. Ландсберг Г.С. Общий курс физики, т.111, Оптика, М., Гизтехникотеорлитературы, 1957.
15. Свентицкий И.И. Закон электромагнитной инерции Ленца и феноменалььные принципы физики. // Электротехника. 2003, N8. - с.16-20.
16. Яворский Б.М., Детлаф А.А. Справочник по физике. - М., Наука, 1980.
17. Базаров И.П. Термодинамика. - М., Выш.Школа, 1976.
18. Зотин А.И., Зотин А.А. Направление, скорость и механизмы прогрессивной эволюции. - М.: Наука, 1999.
19. Бушуев В.В., Голубев В.С. Основы эргодинамики. - М., Энергия, 2003.
20. Хайтун С.Д. Механика и необратимость. - М., "Янус", 1996.
21. Блохинцев Д.И. Основы квантовой механики. Издание четвертое. - М., Высшая школа, 1963.
22. Голицын Б.Б. Ученые записки Московского университета, N10, т.1, М., 1893. Избранные труды, 1, М., 1960.
23. Заев Н.Е., Спиридонов Ю.С. Емкость - конвертор тепла среды в электроэнергию. // Электротехника, 1998, N12. - с.53-55.

Вернуться в список круглого стола на fips-03.htm
  ©   16.04.2004  Шестопалов А.В.